新学期もそろそろスタート。皆さんも新たな気持ちで数学の勉強に取り組もうとされていることと思います。
今回は曲線の接線について考えてみたいと思います。接線というとどんな直線を思い出しますか？ 昔からこの曲線の接線について、いろいろな定義が考えられて来ました。
まず一番おなじみの接線と言えば、円の接線ですね。古代ギリシアで、円の接線は「円とただ１点を共有する直線」と定義されました。
中学でも「円」の章で円の接線についてこう習いましたね。
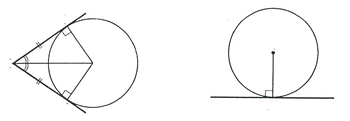
中学の「円」で接線の性質、「円外の１点から引いた２本の接線の長さは等しい」や、「円の接線は接点を通る半径に垂直である」などを勉強しました。
後半の性質を使うと円の接線は簡単に引くことが出来ます。
では円以外の曲線についてはどう考えたら良いのでしょうか？ 円の接線のように「ただ１点のみを共有する」という定義だと図のように接線とは言えない直線が引けてしまいます。
確かに１点のみを共有していますが曲線と交わってしまうものや、接線でも曲線と２点以上共有しているもの、などです。
こんなわけで曲線の接線のとらえ方について別の方法が考えられました。
接線の特徴を利用した方法として次の方法が考えられたのです。曲線上の接点Pとそれ以外にもう１点Qをとり、２点を直線で結びます。この点Qを点Pにどんどん近づけていくと、直線PQは点Pでの接線に近づいていくと考えられるのです。
この考え方によって曲線の接線の考え方は円以外の曲線にも使えるということが何人もの人によって研究された後17世紀にニュートンによって明確に定義され、理論による曲線の接線をとらえることができたのです。
即ち、
「次の図のように、曲線上に２点P , Q をとり、直角三角形P Q R をつくる。このとき、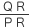 は直線P Q の傾きで、点Q を点P に限りなく近づけていき、直線P Q が近づいていくような直線が存在するとき、この値は点Pにおける曲線の接線の傾きである。」というものです。
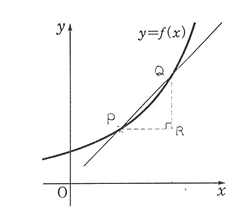
接線の傾きを求めることによって、曲線の曲りぐあい、つまりある関数の表す曲線上のそれぞれの点において上向きか下向きか（関数の値が増加しているか減少しているか）、曲線が上に膨らんでいるか下に膨らんでいるか（上に凸か下に凸か）などが分かるようになりました。また物理では物体の運動の様子を縦軸に距離、横軸に時間を取った場合、その物体のそれぞれの瞬間における速度や加速度などを数式で表せるようになり、今日の数学と物理学の基礎が確立されました。接線とはとても大事な直線だったんですね。
|
