数学の問題を解く時に計算を出来るだけ簡単にする工夫は、間違えるのを避けるために大切なだけでなく、解く時の楽しみでもあります。今回はその一例として図形の工夫を中心に考えていきましょう。
例題1、次の図のような正四角柱を一つの平面で切った立体の体積を求めなさい。
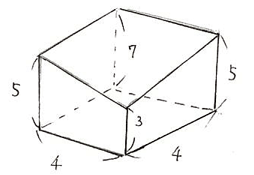
解答:与えられた図形と合同な図形を図のように逆さにして重ねると高さが10の 正四角柱になります。よって、
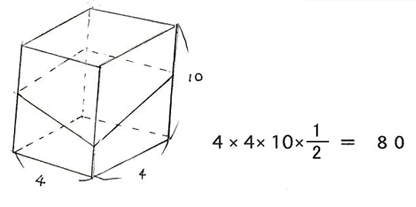
例題2、次の図の斜線部分の面積を求めなさい。
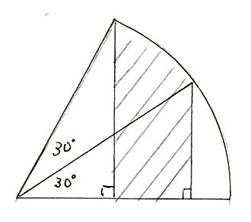
解説:図のアとイの部分の面積が等しくなるので、求める面積は、中心角30°の扇形の面積が求める面積となります。
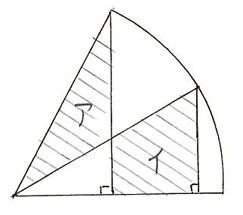

(慶應義塾大学薬学部)
|

