
まず、「中点連結定理」について確認しておきましょう。
<中点連結定理>
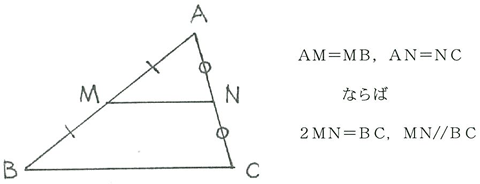
三角形ABCにおいて、底辺BC以外の 2 辺AB,ACの中点をそれぞれM,Nとおく。このとき、MNと底辺BCの間に 2MN=BC かつ MN//BC が成り立つ。
「中点連結定理の逆」というのもあります。
<中点連結定理の逆>
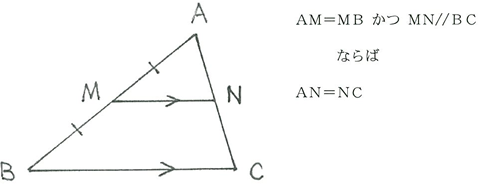
三角形ABCにおいて、辺ABの中点Mから引いた底辺BCの平行線と、残りの辺ACとの交点Nは、辺ACを二等分する。
では、問題を解いていきましょう。
はじめは、相似な三角形をさがしてみましょう。手がかりは「平行線」。
「平行線」あるところに「相似」ありです。
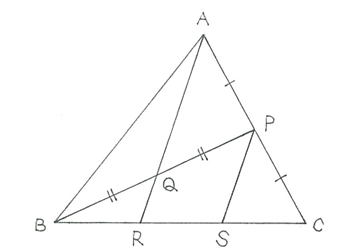
この図のなかで平行線といえば、ARとPSです。ARとPSを、またはそれらの一部を辺として持つ三角形を調べます。すると、△CARと△CPSが相似であることがわかります。
△CARにおいて、辺CAの中点Pから引いた底辺ARの平行線がPSですから、中点連結定理の逆より、点Sは辺CRを二等分します。つまり、
RS=SC ・・・・・・①
次に、△BPSを見ると、QRとPSが平行で、点Qは辺BPの中点ですから、ここにも中点連結定理の逆が使えます。よって、点RはBSを二等分する点なので、
BR=RS ・・・・・・②
①、②より
BR=SC
であることが証明されました。
図形の問題で、何から考えていいのかわからないときは、相似な三角形をさがしてみましょう。そのときは、平行線に注目ですよ。 |
