開成中に合格した子たちはおそらくこの問題はできているだろう。ここでは御三家レベルの子たちがするであろう解法を紹介したい。基本的なこと（例えば、同じ距離では速さの比とかかる時間の比が逆比になることや連比の考え方とか。）はすべてわかっているものとする。最短の解き方を紹介しよう。
まず、下のようなダイヤグラムを描けなければならない。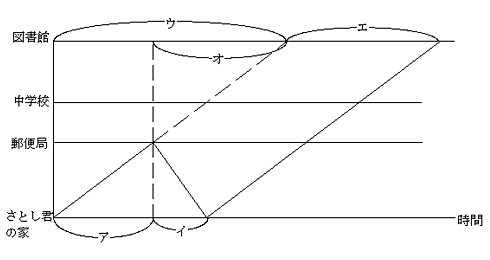


このア〜オに数値を代入すればよい。
まず、ア：イは郵便局に行って戻るまでの時間の比であるから
ア：イ＝３：２
ウ；エは予定の時間と余分にかかった時間の比であるから
ウ：エ＝1：1.1＝10：11
エとア＋イは同じ長さであるから、ここで比の値をそろえます。そうすれば、アとウの値はくらべられます。
５と１１の最小公倍数は５５であるから
ア：イ＝33：22　　ウ：エ＝50：55
オ＝50−33＝17
ア：オ＝33：17
ア：オは、さとし君の家から郵便局までと、郵便局から図書館までの距離の比ですよ。
これでさとし君の家から郵便局までと、郵便局から図書館までの距離の比が、33：17であることがわかりました。

次に、図書館からさとし君の家に帰る時のダイヤグラムを描きます。


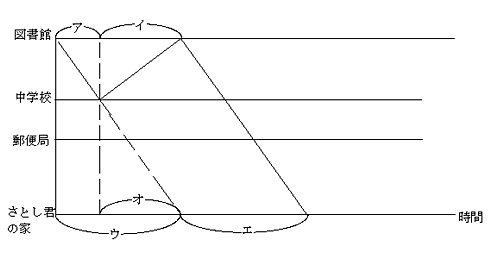
これも全く同様に解きます。
ア：イ＝２：３
ウ：エ＝1：0.7＝10：7
エ＝ア＋イより
ア：イ＝14：21　ウ：エ＝50：35
オ＝50−14＝36
ア：オ＝14：36
ア：オは、図書館から中学校までと、中学校からさとし君の家までの距離の比です。
これで図書館から中学校までと、中学校からさとし君の家までの距離の比が14：36であることがわかりました。
もう答えは出たも同然ですね。
ここまでわかったことを図に表すと下のようになります。図を見てわかるように郵便局と中学校の間は比の３に相当することがわかります。

比の３が９０ｍになりますから比の１は３０ｍ
３０×５０＝１５００ｍ……さとし君の家から図書館までの道のり
３０×３３＝９９０ｍ……さとし君の家と郵便局の間の道のり